How Does the Angle of Lift Affect the Lifting Capacity of a Lifting Sling?

In the area of lifting operations, the knowledge of the mechanisms of lifting slings is indispensable for safety and productivity assurance. An angle of the lift is one of the most influential factors, which determines lifting ability of usage of a sling. This paper aims to analyze the effect of the angle at which a sling is operated on the lifting capacity of the rope.

I. Mechanical Principle: Force Decomposition Based on Lifting Angle

1.Basic Force Model
When an object is lifted by slings, the gravitational force (G) decomposes into tension (F) along the sling direction. For a two-sling setup (with the angle θ between the sling and the vertical), the tension on each sling can be calculated via vector decomposition:

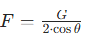
Here, the larger θ is (i.e., the more horizontal the sling), the smaller the value of cosθ, and the greater the tension F on the sling.

2.Case Demonstration

·When θ = 30°, F = G/(2×0.866) ≈ 0.577G;

·When θ = 60°, F = G/(2×0.5) = G;

·When θ = 80°, F = G/(2×0.174) ≈ 2.87G.
Evidently, as θ increases from 30° to 80°, the sling tension surges from 0.577G to nearly 3G, significantly reducing the lifting capacity.

II. Specific Impacts on Lifting Capacity

1. Relationship Between Sling Tension and Rated Load

·The rated load (Safe Working Load, SWL) of a sling is set based on vertical lifting (θ = 0°, where F = G/2). As θ increases, if the actual tension exceeds the rated load, the sling may break due to overload.

·Example: A sling with a rated load of 10 tons (for vertical lifting) can only lift 10 tons × 2 × cos60° = 10 tons when θ = 60°. When θ = 80°, the allowable lifting weight drops to 10 tons × 2 × cos80° ≈ 3.47 tons to avoid overload.

2. Reduction in Safety Factor

·Slings are typically designed with a safety factor (e.g., 5:1 or 6:1), meaning the rated load is 1/5 or 1/6 of the breaking force. As θ increases and the actual tension approaches the breaking force, the safety factor drops drastically, increasing the risk of failure.

3. Uneven Loading and Local Wear

·In multi-sling setups, inconsistent angles cause uneven tension (e.g., slings with larger θ bear more force), leading to overload on some slings or accelerated wear due to stress concentration.

III. Industry Standards and Safety Recommendations

1.Angle Limitation Criteria

·Most industry standards recommend keeping the lifting angle θ (from the vertical) ≤ 60°, where the sling tension is F = G, maintaining a reasonable safety factor.

·Some specifications (e.g., crane operation manuals) strictly require θ ≤ 45° for higher safety margins.

2.Sling Selection and Angle Control

·Calculate load based on angle: Use the formula to ensure F ≤ rated load before lifting.

·Use auxiliary tools: Adjust angles with lifting belts or balance beams to avoid excessive sling inclination.

·Monitor angle changes: Dynamic lifting (e.g., object swaying) may instantaneously increase θ, requiring prior risk assessment.

3.Differences Between Sling Types

·Wire rope slings: Stiffer, with more direct impact of angle changes on tension; angle control is critical.

·Synthetic fiber slings: More flexible but prone to internal fiber wear from compression at large angles, reducing strength.

IV. Practical Considerations

·Avoid horizontal lifting: When θ = 90° (horizontal sling), theoretical tension F→∞, making lifting impossible—this must be strictly prohibited.

·Symmetric lifting: Ensure symmetric angles in two-sling or multi-sling setups to prevent uneven loading.

·Regular inspection: After lifting at large angles, check slings for deformation, wear, or broken wires to maintain safety.

Conclusion

The lifting angle affects the actual carrying capacity of slings by altering the tension. A larger angle increases tension and reduces lifting capacity. In practice, mechanical calculations, angle control, and compliance with safety standards are essential to ensure slings operate within a reasonable angle range and avoid overload risks.